Математические задачи играют огромную роль в процессе обучения математике. При обучении их решению стоит знать ответ на вопрос: Какие функции они играют в процессе обучения математике? Ответ не прост, можно сказать, что математические задачи служат средством закрепления полученных знаний и выработки конкретных умений, они являются инструментом проверки результатов обучения, с их помощью мы можем показывать приложения математики, развивать воображение, логическое мышление, и учить математическим рассуждениям. Задачи обычно имеют множество различных способов решения, они могут показать учащимся математику не только как набор определенного содержания и определенных умений, но прежде всего учат активному подходу к различным практическим задачам.
Общие мыслительные операции, полезные при решении задач, по порядку, список вопросов и подсказок. Четыре этапа работы: I. Понимание задачи. Учащийся должен бегло сформулировать задание. В нем должны быть указаны основные элементы задания: неизвестно, дано и условие. Вопросы: «Что неизвестно?», «Что дано?», «Какое условие?». Если с заданием связана определенная фигура, учащийся должен сделать рисунок и указать на нем неизвестное и данные. Он должен ввести соответствующие обозначения с некоторым вниманием к правильному выбору символов. II. Посмотрите, как отдельные величины связаны друг с другом, как неизвестное объединяется с данными, чтобы составить некоторое представление о решении и составить определенный план. Материалы, необходимые для решения математической задачи, — это определенные элементы ранее приобретенных математических знаний, например, ранее решенные задачи или ранее доказанные теоремы. Поэтому принято начинать работу над задачей с вопроса «Знаете ли вы какую-нибудь родственную задачу?», «Знаете ли вы какую-нибудь теорему, которая может быть здесь полезна?». Подсказка для выбора связанной задачи: «Посмотри на неизвестное! И попробуй вспомнить какая-то хорошо известная задача с таким же неизвестным». Если учащийся смог вспомнить ее, из нее можно многое извлечь». Вот ранее решенная задача, связанная с вашей проблемой. Не могли бы вы использовать его?», «Не могли бы вы использовать метод, использованный в нем?». Если вышеперечисленные вопросы не помогают, то нужно поискать другие точки соприкосновения и изучить различные аспекты задачи. Мы должны менять, трансформировать и модифицировать задачу. "Не могли бы вы переделать задачу по-другому?" "Не могли бы вы придумать более доступную родственную задачу? Более общую задачу? Более конкретную? Аналоговую? Не могли бы вы решить часть проблемы? Оставьте только часть условия, отбросьте остальное. В какой степени неизвестное тогда определено, как оно может тогда измениться?». Пытаясь использовать различные известные задачи или теоремы, рассматривая различные модификации, экспериментируя с различными вспомогательными задачами, мы можем отойти от исходной задачи. III. Выполнение плана. План дает нам грубый набросок решения. Ученик должен убедиться, что все детали вписываются в этот эскиз. При выполнении плана учитель должен настаивать на том, чтобы ученик проверял каждый шаг своих действий. Важно, чтобы ученик был убежден в правильности каждого шага. В некоторых случаях учитель может подчеркнуть разницу между «видеть» и «доказывать»: «Ясно ли вам, что этот шаг вашего рассуждения верен? И не могли бы вы также доказать, что этот шаг верен?» IV. Взгляд назад. Оглядываясь на данное решение, переосмысливая и анализируя результат и путь к нему, ученики могли закрепить свои знания и развить способность решать задачи. Учитель должен внушать мысль о том, что ни одна проблема не может быть полностью исчерпана. Достаточно тщательно изучив проблему, мы можем улучшить любое решение и, в частности, улучшить понимание решения. Учащийся мог допустить ошибку, поэтому желательна отметка «Можете ли вы проверить результат? Можете ли вы проверить обоснование решения?», «Можно ли получить результат другим способом?». Мы предпочитаем краткое и интуитивно понятное решение длинному и утомительному «Можете ли вы осветить его с первого взгляда?». Преподаватель должен побуждать учащихся думать о случаях, когда они могли бы использовать метод решения, использованный здесь, или само решение «Можете ли вы использовать результат или метод решения для другой задачи?». В то время как цель задачи состояла в том, чтобы найти определенный объект, неизвестное задачи, в то время как ее основными частями были: неизвестное, данные и условие, а вопросы и подсказки содержались в упомянутом выше списке, цель задачи «доказать» состоит в том, чтобы надежно продемонстрировать, что некоторое четко сформулированное утверждение является истинным или ложным. Если задача «доказать» — это обычная математическая задача, то ее основными частями являются предположение и тезис теоремы, которую мы должны доказать или опровергнуть. Есть полезные вопросы и советы по этим частям, соответствующие вопросам и список, специально предназначенный для поиска заданий: «Что такое посылка? Что такое тезис? Разделите части посылки. Найдите связь между посылкой и тезисом. Посмотрите на тезис. известная теорема, в которой содержится такой же или похожий тезис. Оставьте только часть предположения, отбросьте остальные. Действителен ли тезис? Не можете ли вы получить что-то полезное из предположения? Не можете ли вы рассмотреть другое предположение, из которого вы может легко вывести тезис? Не можете ли вы изменить предположение или тезис так, чтобы новая посылка или новый тезис были ближе друг к другу? Вы использовали всю посылку?" Учащийся, уже самостоятельно решающий задачи, начинает чувствовать себя математиком своего дела, отдается очарованию преодоления трудностей. Это очень важный момент во «встречах с математикой». Активизация этого типа может способствовать созданию нового подхода к предмету, развитию интересов и уверенности в себе. Нам нравится ощущение, что мы преодолели препятствие. Он хочет продолжать это делать, и чем больше он это делает, тем лучше у него это получается. Такую возможность мы создаем для учащихся на уроках математики, ставя перед ними задачи, требующие творческого акта и своеобразного изобретательства, и вырабатывая новые элементы их деятельности. | |
| Категория: Калейдоскоп различных знаний | | |
| Просмотров: 14097 | |
Решаем математические задачи
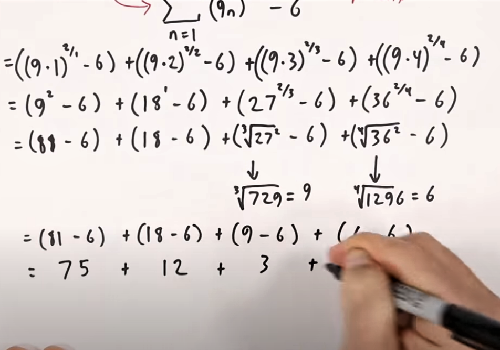 Преподаватель должен помогать учащемуся в решении задач, но не слишком много и не слишком мало, чтобы учащемуся оставалась соответствующая, продуманно подобранная часть работы. Эта помощь должна быть сдержанной, ненавязчивой, если ученик мало что может сделать.
Преподаватель должен помогать учащемуся в решении задач, но не слишком много и не слишком мало, чтобы учащемуся оставалась соответствующая, продуманно подобранная часть работы. Эта помощь должна быть сдержанной, ненавязчивой, если ученик мало что может сделать.